고유값과 고유벡터 (eigenvalue and eigen vector)
Ax = λx 행렬 A를 총괄적으로 나타낼수 있는 하나의 특수한 값을 고유값(eigen value) 라고 한다. 그리고 고유값에 따른 벡터 x를 고유 벡터(eigen vector) 라고 한다. 고유값은 특수한 값인데, 그렇다고
jubrodev.tistory.com
대각화(Dianalization)
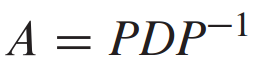
다음과 같은 식에서 P는 invertible 하고, D는 대각행렬(diagonal)이다.
우리가 전 글에서 봤듯이 Similar한 형태의 식과 비슷한데 그 식에서 B가 대각행렬이 되면, A는 대각화 가능하다고 하는것이다.
그럼 당연하게도, 대각화 가능한 A행렬과 대각행렬 D는 SImilar하다.
그럼 왜 굳이 또 복잡하게 저렇게 대각화 하는것인가??
우리가 LU factorization(행렬분해)에서도 느꼈듯이, 행렬을 저 형태로 분해함에 따라 더 계산을 쉽게 하던가 여러 성질을 관찰할 수 있기 때문이다.
예를들어 A의 k승을 계산할때,
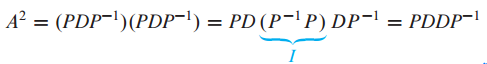

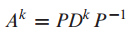
다음과 같이 쓴다면 P와 P의 역행렬끼리 상쇄되고 앞뒤의 P와 P^-1, D의 k승만 남게 된다.
n x n 행렬의 A가 대각화가능하면(Diagonalizable) n개의 linearly independent한 eigen vector를 갖는다.
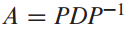
해당식에 양변에 P를 곱하면 아래 식이 된다.
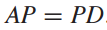
우선 P의 각 column들을 v1 ... vn이라 잡으면 AP와 PD는 다음과 같이 나타낼 수 있다.
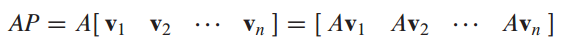
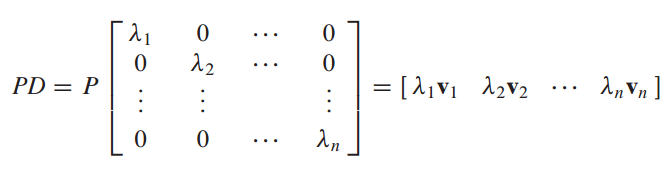
AP = PD를 나타내면 어디선가 많이 봤던 모양새이다.
고유값과 고유벡터에서 Ax = λx에서 고유벡터가 x였다.
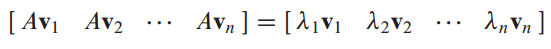
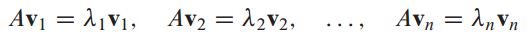
P 행렬은 Linearly Independent 하므로, 각 v들이 Linearly independent하고, n개의 eigen vector가 있다.
그리고 n x n 행렬 A가 n개의 dinstinct eigen values를 가질때 결국 n개의 eigenvector을 가지니, diagonalizable 하다고 말 할 수 있다. 필수적으로 n개가 있어야 하는것이 아니라, 충분조건이다.
'공부 > 선형대수학' 카테고리의 다른 글
| [미분학] Gradient, Divergence, Curl (1) | 2024.09.10 |
|---|---|
| 선형대수학 TF 문제 (0) | 2023.07.03 |
| 고유값과 고유벡터 (eigenvalue and eigen vector) (0) | 2023.06.23 |
| 기저 변환(change of basis) (0) | 2023.06.21 |
| 행렬 분해 (Matrix factorization) (0) | 2023.06.15 |


